


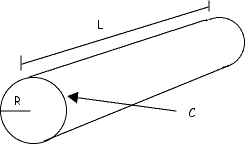
Soit un ver de terre considéré comme un cylindre de volume V, de longueur L, de section S ayant une circonférence C et un rayon R. On nommera P l'aire de la peau (surface cutanée).
La circonférence ( = tour de taille du ver) C = 2∏R
La section S = ∏R2.
L'aire de la peau est P = CL = 2∏RL
Le volume du ver est V = SL = ∏R2L
À longueur égale, quand R est doublé,
1) la circonférence C de la section est doublée et donc l'aire P de la peau est doublée ;
2) la section S et donc le volume corporel V augmentent proportionnellement au carré de R (c'est-à-dire, si le rayon double la section quadruple)*.
Sachant que le lombric a une respiration cutanée, on comprendra aisément que l'intensité respiratoire I sera proportionnelle à l'aire de la peau : I = kP.
On comprendra aisément que les besoins respiratoires (B) du lombric dépendent de sa masse corporelle, laquelle est proportionnelle au volume corporel : B = k'V.
Pour résumer : Quand le lombric s'élargit (sans s'allonger), son intensité respiratoire augmente proportionnellement au rayon : f(R) = aR, mais ses besoins respiratoires augmentent proportionnellement à son carré : f(R) = aR2. Autrement-dit, si le diamètre du ver double, son intensité respiratoire doublera, mais ses besoins quadrupleront.
Conséquence : Si un lombric grossit il risque l'asphyxie.
PS : N'hésitez pas à immobiliser le curseur sur les illustrations.
* NB : Bien sûr, si la longueur et le rayon augmentent simultanément, le volume corporel augmente proportionnellement au cube de la longueur pendant que l'aire de la peau augmente proportionnellement à son carré. Autrement-dit, si les longueurs doublent les aires quadruplent (22) et les volumes sont multipliés par 8 ( = 23). Dans la première démonstration, j'ai considéré que la longueur n'augmentait pas.
Lien externe pour comprendre : Le lombric mathématicien (la page de Thérèse).
Évaluation interdisciplinaire :
1) Si on double l'arête d'un cube, par quel nombre son volume sera-t-il multiplié ?
2) Volume du soleil