Quadrature du cercle - Squaring the circle

Comment dessiner un carré dont l'aire est égale à celle d'un cercle

Un cercle (disque) de rayon unité a la même aire qu'un carré de côté √∏ (racine carrée de Pi).
Aire du cercle = ∏ si R = 1 ; Aire du carré = √∏ x √∏ = ∏
Ce n'est donc pas la démonstration qui est difficile !
Sur ces constructions numériques, l'aire du carré est rigoureusement égale à celle du cercle.

Vouloir résoudre la quadrature du cercle,
c'est l'opération qui consiste à construire un carré de surface rigoureusement équivalente à celle d'un cercle, le tout à l'aide d'une règle et d'un compas.
C'est, nous dit-on, impossible ! (Lindemann 1882)
It is impossible to square the circle

Les Égyptiens considéraient qu'un cercle de diamètre 9 avait la même aire qu'un carré de côté 8..

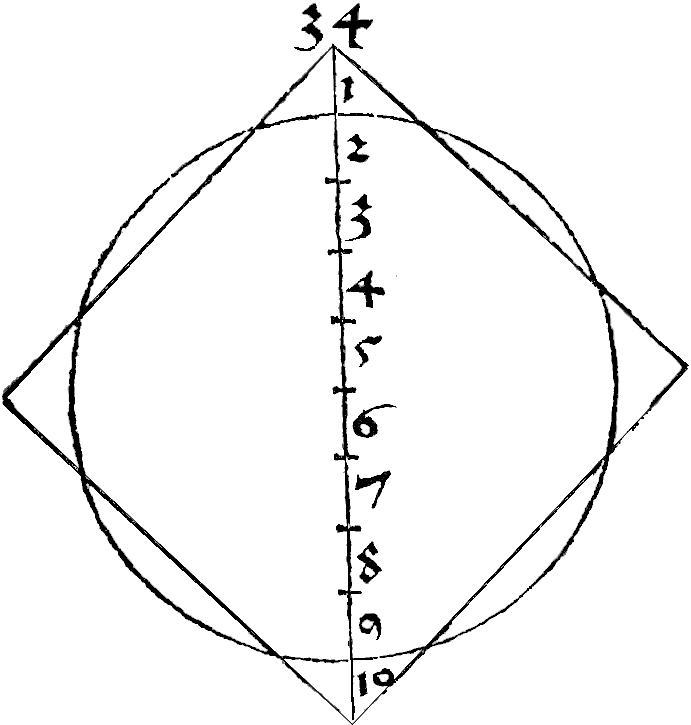
En 1525, Albrecht DÜRER considère qu'un cercle dont le diamètre égale 8 a approximativement la même aire qu'un carré dont la diagonale égale 10.

Je soumets aux internautes ce problème concret : J'ai une boule d'argile de 10 cm de rayon que je voudrais transformer en cube en utilisant un moule. Quel doit être le côté du cube ? Réponse ici

Construire à la règle et au compas les figures montrant l'égalité des aires du cercle et du carré est impossible.
On comprend pourquoi l'expression "chercher à resoudre la quadrature du cercle" veut dire que l'on cherche à résoudre un problème insoluble.

Citations :
"Réussir à réconcilier la base et le sommet équivaudrait à résoudre la quadrature du cercle." (Alain De Malglaive)
"Réussir à réconcilier l'écologie et l'économie équivaudrait à résoudre la quadrature du cercle." (Rémy Gall paraphrasant Alain De Malglaive)
Angela MERKEL aurait dit : "Le cubage de la sphère est encore plus difficile que la quadrature du cercle".

Cercle vient du latin circulus qui est le diminitif de circus qui veut dire cirque. Le grec a un mot pour le cercle : κύκλος et un mot pour le cirque : κίρκος. L'étymologie veut que les cirques soient "ronds". On n'a jamais vu de cirques carrés ! L'élève ne doit pas dire "je dessine un rond", mais "je trace un cercle" ! C'est plus classe !
Certains puristes distinguent le cercle, en tant que circonférence, et le disque en tant que surface plane limitée par un cercle. Le cercle est donc la frontière du disque. Comme le problème de la quadrature du cercle concerne les aires, ne devrions-nous pas dire "quadrature du disque" ?
Disque vient du grec δίσκος qui est un objet discoïde lancé par un athlète appelé Δισκοβόλος.
Revenons à des périodes plus récentes, après la disque vinyle (1948) qui tourne sur un tourne-disque. L'industrie informatique a créé de nouvelles expressions et sigles : Disque compact (CD-audio 1982 et CD-Rom), DVD (Digital Versatile Disc 1995). Le disque dur a été inventé par IBM en 1956 (déjà !).

Parmi les 4 figures présentes sur cette page :
la 1e a été réalisée en javascript par moi-même ; Les javascripteurs regarderont comment j'ai programmé la construction du carré : Racine carrée de ∏ s'écrit "Math.sqrt(Math.PI)" ;
Les 2 figures suivantes en svg sont extraites de Wikipedia ; Le dernière est une copie png d'un dessin d'Albert Dürer.